Дневники чайника. Чтива 0, виток1

Начать хочу с команды деления, а почему именно так - вы узнаете по ходу.

0. Команда деления DIV

Хм... Прошло так много времени, что я опять забыл, на чём остановился...

Ах да, вот последняя фраза из прошлой главы: "Некоторые команды всегда используют определённый регистр в качестве приёмника или источника".

И действительно, большинство команд ассемблера требуют явного указания всех операндов, но есть и такие, которые выполняют действие с жёстко заданными регистрами. А вот и пример.

DIV работает с определёнными пАрами регистров.

Команда DIV

Происхождение	От англ. слова division - деление
Формат	DIV делитель
Действие	Натуральное деление нацело. Вход: Выход: AX /делитель8bit частное AL, остаток AH DX_AX /делитель16bit частное AX, остаток DX EDX_EAX/делитель32bit частное EAX, остаток EDX
Примечание	Команда div призвана делить натуральные числа. Для чисел со знаком используйте команду idiv. Деление на 0 вызывает исключение

Как видите, программист может выбрать лишь расположение и тип делителя.

"Делитель8bit" в этой таблице означает не число 8, а ячейку памяти в 1 байт или 8-битный регистр общего назначения, в котором будет само значение.

Соответственно: "делитель16bit" = 16-битная ячейка, или РОН-16; "делитель32bit" = 32-битная ячейка, или РОН-32.

Помню, долго вникал в общепринятую справочную систему, потому и даю в своих статьях информацию о командах, но этого явно мало. Всё равно необходимо пользоваться полноценным справочником. Где, скорее всего, вы увидите такие обозначения:

r    - регистр (например, mov AL,AH или mov AX,BX и т.п.)
m    - ячейка памяти (например, mov EAX, [00402000])
imm  - непосредственное значение в команде (например, mov EAX,123)

Программа покажет шесть результатов целочисленного деления на 10d чисел 0Ah,0Bh,0Ch,0Dh,0Eh,0Fh.

Даже если пример показался простым и понятным, проследите в отладчике хотя бы за регистром AX при делении.

Помните, в школе учили делить так, чтобы получалось целое число и отдельно неделимая часть? Оказывается, процессор в основном делит так же.

На выходе мы имеем два числа. Слева - остаток, справа - частное.

В этом примере очень много нового и важного для нас.

Начнём снизу.

Команда POPAD в данном примере не обязательна, но тогда нужно удалить и PUSHAD в начале процедуры. Эта пара команд позволяет не потерять значения всех РОН в ходе выполнения функции HexMessage.

С MessageBox мы уже знакомы, она просто показывает строку текста в стандартном окошке.

Но строку с текстом ещё нужно создать. Напомню, в Windows мы будем оперировать ANSIz-строками (соответствующая кодировка и байт 00 - как символ конца строки).

Для получения текстовой строки из числового значения чуть выше мы вызвали API-функцию wsprintf.

Вот её вызов в исходнике prax11:

;                адрес будущей строки| адрес строки формата| число
invoke wsprintf, ADDR sResult,         ADDR sfc,             EAX

Теперь посмотрим на Ассемблер в отладчике:

00401064  50          push eax                     ; /
00401065  68 01304000 push P11.00403001            ; |Format = "%.4lX"
0040106A  68 05304000 push P11.00403005            ; |s = P11.00403005
0040106F  E8 18000000 call <jmp.&user32.wsprintfA> ; \wsprintfA
00401074  83C4 0C     add  esp, 0C

Разбор:

00401064  50          push eax                     ; /

В стек помещается значение EAX (при этом ESP уменьшается на 4).

00401065  68 01304000 push P11.00403001            ; |Format = "%.4lX"

В стек помещается указатель на строку формата функции (при этом ESP уменьшается ещё на 4).

0040106A  68 05304000 push P11.00403005            ; |s = P11.00403005

В стек идёт указатель на строку, куда надо поместить результат (и опять - ESP минус 4).

0040106F  E8 18000000 call <jmp.&user32.wsprintfA> ; \wsprintfA

Вызов функции и возврат из нее (после выполнения стек в данном случае не меняется!).

00401074  83C4 0C     add  esp, 0C

А вот это очень интересная строка.

Командой сложения мы прибавляем к значению регистра ESP нужное число. Таким образом, регистр, указывающий на вершину стека, принимает своё значение до строки 00401064. Стек часто выравнивается именно так.

Мы передавали параметры через стек, и функция отработала их.

Но wsprintf выделяется из общего ряда API именно тем, что не выравнивает стек сама.

Поясню.

Вернёмся собственно к делению.

0Ah/0Ah = 1 частное и остаток 0
0Bh/0Ah = 1 частное и остаток 1
0Ch/0Ah = 1 частное и остаток 2
0Dh/0Ah = 1 частное и остаток 3
0Eh/0Ah = 1 частное и остаток 4
0Fh/0Ah = 1 частное и остаток 5

А теперь сравните с равенством:

0Ah=10d
0Bh=11d
0Ch=12d
0Dh=13d
0Eh=14d
0Fh=15d

Правда, удивительно?

Выходит, делением на десять мы можем получить запись числа десятичными цифрами.

Но тут есть один очень хитрый момент. Сам споткнулся.

Ведь в нулевом витке писал же: всё, что мы видим на экране, - всего лишь представление!

Писал-писал - и сам себя не понял =).

Двоичная система наиболее приближена к физическим свойствам машины. Поэтому попробуем разобрать вопрос через неё.

Итак, допустим, у нас есть число 1Ah. В двоичном представлении будет:

0001 1010

Оно же десятичное 26.

И тут возникает вопрос, почему для цифр "2" и "6" (предположим, в регистре AL) нужны биты:

0010 0110

Почему битовые значения отличаются?

Потому что отладчик и другие подобные программы отображают hex-числа.

Истинный смысл такого перевода целочисленным делением заключается в том, что мы, оставаясь в шестнадцатиричной системе, получаем внешний вид десятичными цифрами.

Такое представление называется двоично-десятичное (на мой взгляд, глупое название, тут оригинальный термин более уместен: BCD - Binary-Coded Decimal).

Так же, как и в hex, каждая десятичная цифра BCD-числа занимает одну тетраду (4 бита).

Только здесь используются не все состояния тетрады:

0000 = 0           1010 = не используется
0001 = 1           1011 = не используется
0010 = 2           1100 = не используется
0011 = 3           1101 = не используется
0100 = 4           1110 = не используется
0101 = 5           1111 = не используется
0110 = 6
0111 = 7
1000 = 8
1001 = 9

Теперь давайте ещё раз взглянем на действия prax11:

0Ah/0Ah -> AX = 00 01
0Bh/0Ah -> AX = 01 01
0Ch/0Ah -> AX = 02 01
0Dh/0Ah -> AX = 03 01
0Eh/0Ah -> AX = 04 01
0Fh/0Ah -> AX = 05 01

Немножко недотягивает до 10,11,12...

Что же нужно сделать?

Для начала поменяем местами значения регистров AH и AL.

Вообще говоря, для этого существует команда XCHG.

Работает она так:

xchg   AH, AL    ; Поменять значения регистров местами

Но в данном случае (как обычно =) есть более компактный способ.

Дело в том, что для работы с BCD-числами предусмотрены 4 специальные команды (AAA,AAD,AAM,AAS).

Деление на 10d с целью получить BCD-представление числа выполняется так часто, что для этого ввели новую команду.

Команда AAM

Происхождение	от англ. ASCII Adjust AX After Multiply - ASCII коррекция АX после умножения
Формат	AAM (не документировано: AAM делитель)
Действие	Натуральное деление нацело для коррекции десятичных представлений чисел. Вход: Выход: AL/10 частное AH, остаток AL не документировано: AL/делитель8bit частное AH, остаток AL
Примечание	При делителе = 0 вызывает исключение

Из таблицы видно, что процессор умеет выполнять операцию AAM не только с делителем 10d. Эта возможность не документирована производителями, но соответствующие коды Интел-совместимые выполняют на ура.

Правда, компилятор MASM не знает об этом, так что если нужно использовать недокументированные команды, приходится вставлять в исходник не мнемоники, а коды таких операций (или использовать FASM =).

Получается, главное отличие AAM от DIV (не считая размера делителя) - другое расположение результата.

Сделайте так: скопируйте prax11.asm (допустим, в prax11b.asm) и измените там все строки:

	div    byte ptr [divisor]

на

	aam

Результат должен быть вот таким:

0Ah/0Ah -> AX = 01 00
0Bh/0Ah -> AX = 01 01
0Ch/0Ah -> AX = 01 02
0Dh/0Ah -> AX = 01 03
0Eh/0Ah -> AX = 01 04
0Fh/0Ah -> AX = 01 05

Такой вид называется непакетированной двоично-десятичной записью числа. Во наворотили!.

А суть-то элементарная.

Остаётся избавиться от лишних нулей, "сомкнув" разряды в одном байте, и мы получим пакетированное BCD-число.

Для этого предлагаю добавить две команды в процедуру HexMessage перед вызовом wsprintf:

rol  AL,4
ror  AX,4

Попробуйте.

Команды ROL и ROR перемещают биты в регистрах "по кругу".

Допустим, было:

     AH AL
AX = 01 04

Представим в битах:

   AH          AL
0000 0001   0000 0100

"Rol AL,4" переместит биты влево на 4 шага. При каждом из четырёх перемещений старший бит становится младшим.

        AL
0<1<0<0 < 0<0<0<0<
|________________^

Теперь AX=0140 вместо 0104.

   AH          AL
0000 0001   0100 0000

Осталось перетащить биты всего регистра AX обратно - "ror AX,4":

                   AX
>0>0>0>0 > 0>0>0>0  >  0>0>0>1 > 0>1>0>0
^______________________________________|

И вот наконец-таки желаемое AX =0014.

Но учтите, что с точки зрения ЦП это 14h, а не 14d.

Собственно говоря, в том и заключается главное отличие пакетированной записи от непакетированной.

Ведь за целое можно взять минимум один байт (а тетраду никак нельзя). И получается: в байте с пакетированным представлением чисел старше 9 начинается расхождение чистых двоичных и BCD-чисел.

Теперь мы знаем, как, оставаясь в hex-системе, трансформировать одну цифру от 0 до F в одну или две десятичные цифры. Интересно, а работает ли фокус с целочисленным делением для многозначных чисел?

Некоторые, наверное, знают (а остальные узнают чуть ниже), что в позиционном методе записи значение цифры в числе точно определяется при помощи двух величин - основания и разряда. Выходит, что позиционные системы двухмерны.

Деление/умножение пришло в алгебру именно из трансформации прямоугольников (двухмерных объектов).

Разрезать квадратный кусок ткани на полоски - разделить.

Сшить из полосок прямоугольное покрывало - умножить.

Если немножко расширить и обобщить алгоритм prax11, то мы получим красивый способ представления целого числа а в системе с основанием p:

1. Разделим целочисленным способом a на p (в результате частное замещает a)

2. Остаток запишем очередным разрядом X

3. Если a>0, то переходим на шаг 1

4. Иначе искомое значение найдено (все разряды X справа налево).

p здесь - любое целое число больше единицы.

Вычисления проводятся в исходной системе, то есть базовым будет старое основание a.

a может быть в позиционной системе с основанием больше p (если равно p, то действие бессмысленно, если меньше p, то в базовой системе просто не хватит цифр для записи числа).

Посмотрите, с чего начинается обучение у Кнута.

В первой же главе он знакомит нас с алгоритмом Эвклида.

Как говорится, найдите 10 отличий (специально не указываю, в какой системе 10 ;).

До сих пор мы встречались только с натуральными числами и нулём, теперь пришло время узнать, как в наших компьютерах представляются числа со знаком (+ или -).

Вообще говоря, каждый из нас может придумать свой способ кодирования данных, в том числе и отрицательных чисел, или выбрать что-нибудь из уже придуманного (для примера посмотрите в поиске Коды Грея).

Ничего не мешает использовать несколько команд для какой-нибудь операции над любой последовательностью бит в байте. Но сейчас мы говорим о том, что предложено нам наготово.

Процессор использует так называемый допкод - дополнительный способ кодирования для чисел со знаком.

Он дополняет прямой код, с которым вы уже знакомы... Правда, забыл сказать кое-что ещё про ноль.

Вот значение обычного байта в двоичном виде:

0000 0000

Такое значение в архитектуре Intel считается положительным.

Да-да, в логике целочисленных операций допущена грубая хитрость. 0 - это положительное значение.

Вот где спрятан источник ошибки на один, об этом мы поговорим ещё не один раз =).

Прибавим единицу:

0000 0001

Получилось число 1, а как нам представить "-1"?

Попробуйте отнять два:

mov AL,1
sub AL,2         ; вычесть 2 из значения AL

;или так:
mov AL,1
dec AL           ; отнять 1 от значения AL
dec AL           ; отнять 1 от значения AL

;А можно и так:
mov AL,1
add AL,-2        ; прибавить (-2) к значению AL

В битовом представлении должно получиться:

1111 1111

Это и есть "-1".

Но как же так, спросите вы, ведь это самое старшее значение байта = 255d = FFh.

Да, оно самое. Одновременно и "-1", и "+255".

Таким образом, трактовку значений задаёт программист.

Если мы хотим работать с положительным числом, то нужно использовать команды вычислений без знака. А если данное выше значение мы считаем отрицательным, то нужно использовать команды, учитывающие знак (благо, что таких команд не очень много).

Каждый знаковый байт может иметь значения от "-128" до "+127".

Выходит, половину значений мы условно называем положительными (0...7Fh), а другую половину отрицательными (FF...80h).

Если представить в двоичной системе, получается:

Положительные:

0000 0000 = 0
0000 0001 = 1
...
0111 1111 = 127d

Отрицательные:

1111 1111 = -1
1111 1110 = -2
...
1000 0000 = -128

Старший бит назвали знаковым, так как он определяет знак числа. Если этот бит выключен, то значение в любом случае находится в положительном диапазоне.

Только если старший бит =1, можно трактовать значение как отрицательное число или беззнаковое положительное.

Разумеется, если целое значение не байт, а, например, dword, то всё равно именно старший бит всего значения будет знаковым (бит 31, или 15, или 7 - в dword, или word, или byte соответственно).

Обратите внимание на то, что отрицательные значения идут зеркально положительным.

С этой точки зрения все состояния байта можно описать так:

Hex-значения:             FF............  80|7F ............0

Dec-значения со знаком:   -1............-128|127............0

Dec-значения без знака:  255................................0

Так сделано, чтобы процессоры могли вычитать складывая.

Рассмотрим на примере:

32+ (-22) = 10

Запишем в двоичных числах в столбик:

  32d         0010 0000
+            +
(-22d)        1110 1010
-----         ---------
  10      (1) 0000 1010

ЦП выполнил сложение битов, и получилось значение:

1 0000 1010b

Старший бит не укладывается в байт, и если бы складывались два беззнаковых числа, то пришлось бы задействовать ещё один байт.

Но мы трактуем одно из значений как отрицательное число. В таком случае если просто выкинуть "выползший" старший бит (как будто бы его и нет), процесс сложения совершает вычитание!

Вот такие битовые фокусы.

- В основе космологии бинарии лежит предположение, что пустота позитивна.

- Они не боятся неопределённости, они вообще не знают, что это такое.

- Но зато они боятся зеркал.

- Бинарники говорят: в зеркале мы хуже, чем есть на самом деле, но истинная причина такой неприязни кроется глубже.

- Их вера в то, что за гранью зеркал находятся отрицательные образы, сводит с ума.

Раз положительные значения идут зеркально отрицательным, мы легко можем поменять знак числа.

Достаточно "подставить зеркало".

Инвертируем значение каждого бита. Для этого существует команда NOT:

not  AL         ; к примеру, если AL был 0, то станет 1111 1111b

Однако, как мы только что узнали, состояние байта 1111 1111b представляет знаковое "-1", а не "0".

Вот и нулевой случай ошибки на один.

Рассмотрим работающий пример преобразования отрицательного числа в положительное:

mov  AL, 0FAh   ; AL = FA = 1111 1010
not  AL         ; AL = 05 = 0000 0101
inc  AL         ; AL = 06 = 0000 0110
...

NOT инвертирует значение каждого бита (0 в 1, 1 в 0).

А вот плюс один, выполняемый INC, нужен для восстановления симметрии.

Ведь я особо заметил: ноль приходится считать положительным, тогда в двоичном зазеркалье он становится отрицательным числом, это и нарушает баланс.

Зеркало, которое мы ставим между отрицательными и положительными числами, должно было бы "разрезать" ноль на две части. Но такого не может быть.

Значит, нужно либо вводить в систему 2 нуля (положительный и отрицательный), либо каждый раз подправлять отражение.

Для гармонии, к которой стремится мой разум, и то, и другое плохо, но объяснить тупому пню, что такое неопределённое состояние в виде числа ноль, пока что не получается (пробовал паяльником, потом электромагнитом, потом кувалдой... А, всё равно старый был).

Обратите внимание.

Поскольку рост отрицательных значений идёт зеркально, обратное преобразование выполняется точно так же:

...
not  AL         ; AL = F9 = 1111 1001
inc  AL         ; AL = FA = 1111 1010

То есть опять прибавляется "единица симметрии".

Осознать знаковый бит довольно трудно именно потому, что он выполняет двойную роль:

- двоичное значение в числе;

- флаг знака.

Но надеюсь, после энного прочтения и десятка экспериментов в отладчике читатель всё же воскликнет: Я ПОНЯЛ!

Смотрите так же в справочниках описание команды NEG.

Вы уже знаете, что программы Win32 используют набор символов под названием "ANSI ASCII". Этот набор так называется, потому что он принят Американским институтом национальных стандартов (American National Standards Institute). А в DOS мы использовали кодировку стандарта "IBM ASCII" (её также называют OEM).

Если внимательно посмотреть на таблицы символов, можно заметить, что все различия между ANSI и OEM находятся в старшей половине значений (коды 80-FFh). То есть необходимые символы для отображения hex-числа (1-9, A-F,a-f) кодируются и в DOS, и в Windows одинаково (про Unicode пока промолчим).

Теперь попробуем понять, какую задачу нам предстоит решить.

Начнём с того, что в одном байте закодирован только один ASCII-символ, но hex-разрядов в байте - два.

Кроме того, какие-то "умные" люди решили расположить коды символов так:

30h = 0011 0000b - символ "0"
31h = 0011 0001b - символ "1"
32h = 0011 0010b - символ "2"
...
39h = 0011 1001b - символ "9"
...
41h = 0100 0001b - символ "A"
42h = 0100 0010b - символ "B"
43h = 0100 0011b - символ "C"
44h = 0100 0100b - символ "D"
45h = 0100 0101b - символ "E"
46h = 0100 0110b - символ "F"

Почему разработчики международного стандарта не учли, что представлять числа придётся очень часто, - мне совершенно не понятно. Но стандарт есть стандарт, и с ним придётся мириться.

Получается, для того чтобы создать строку текста из числа, нужно проделать некоторые действия. Такие действия удобно реализовать в отдельной функции.

Эта задача только на нулевой взгляд кажется элементарной, на самом деле существуют сотни решений только на Асме для IA-32.

Каждый приличный программист изобретает этот велосипед хотя бы в одном варианте. Зачем?

Дело в том, что людям нужен не только самый короткий путь, но и путь, по которому можно пройти без лишних усилий. И конечно, самый надёжный путь. А также тот путь, что можно быстро построить и легко модернизировать, - просто красивый и понятный путь. Конечно, чаще всего мы ищем компромисс.

Это и называется оптимизация. По скорости, по размеру, по стабильности, по мобильности и читаемости кода.

- Современные процессоры выполняют миллиарды команд в секунду. Максимальная скорость - это самая сложная оптимизация. Она имеет смысл только в критических вычислениях, которые участвуют в циклах реального времени или очень часто повторяющихся функциях (миллионы и миллиарды раз).

- Размер кода для PC может быть важен в тех случаях, когда нам нужно исправлять уже скомпилированный код (вирусы/антивирусы, патчи/заплаты и т.п.).

- Стабильность важна в любых задачах, но максимальная стабильность требуется в системных программах, которым приходится "выдерживать" бесконечные ошибки программистов и атаки недоброжелателей. Чем более открыта система, тем большую роль играет стабильность каждой отдельной функции. И наоборот: прошивка утюга может быть построена с большим количеством оговорок... Если, конечно, утюг не поддерживает Bluetooth =).

- Главный принцип разработки функций - разделяй и властвуй. Иными словами, каждая единица кода должна как можно меньше зависеть от остальных. То есть иметь свои независимые данные и общаться с внешним миром только через "дверку" (вход-выход). Мобильность помогает быстро использовать процедуры в разных проектах на разных языках.

- Читабельность кода компьютеру не нужна, она ему даже мешает, но исходники пишутся людьми и для людей. Поэтому сегодня появляется всё больше и больше задач, при решении которых прежде всего важна понятность кода.

Разумеется, начинать лучше с простого и понятного.

Но я предлагаю вам компромиссный вариант. Иначе зачем нам вообще Ассемблер?

Реализация

Сегодня, вопреки обычным примерам, мы пройдём по этапам разработки от задачи до решения. Возможно, такой способ разбора примеров будет удобнее.

По сути функция - это самостоятельная программа. Значит и разрабатывать её нужно по тем же правилам.

Этап I. Постановка задачи

Нужно обрабатывать большое количество байт по следующей схеме:

Был 1 байт:         Стало 2 байта:
00          ->      30h, 30h 
01          ->      30h, 31h
...              
09          ->      30h, 39h
...
99h         ->      39h, 39h


0Ah         ->      30h, 41h
0Bh         ->      30h, 42h
...
FFh         ->      46h, 46h

Этап II. Алгоритм

Подробно разрабатывать всё нет смысла, но описать главные действия будет полезно.

Входной байт назовём а.

Результат - X₁, X₂, так как на выходе будет два байта.

Итак:

1.	Выделить из a две части. a1 - старший разряд, a2 - младший

2.	Если  a1 > 9, то X1 = a1+37h 

3.	Иначе X1 = a1+30h

4.	Если  a2 > 9, то X2 = a2+37h 

5.	Иначе X2 = a2+30h

Этап III. Кодирование

До выделения частей значение a лучше загрузить в какой-нибудь регистр общего назначения.

Оперативные действия прежде всего производят в EAX:

movzx EAX, byte ptr [a] ; допустим, AX = 00E5h

Теперь можно разделять тетрады:

rol   EAX, 4            ; AX = 0E50h
ror    AL, 4            ; AX = 0E05h

На этом этапе у нас есть a₁ в регистре AH и a₂ в AL.

Осталось только сложение с условием "Если/иначе".

cmp    AH, 9            ; сравниваем с девятью
jbe    DecDigit         ; если не больше, то прыг
add    AH, 7            ; иначе корректируем символы от A до F
DecDigit:
add    AH, 30h          ; получаем код символа

И, разумеется, не забудем сохранить результат:

mov [X1], AH

Теперь повторим действия для a₂:

cmp    AL, 9            ; сравниваем с девятью
jbe    DecDigit2        ; если не больше, то прыг
add    AL, 7            ; иначе корректируем символы от A до F
DecDigit2:
add    AL, 30h          ; получаем код символа

Cохраняем результат:

mov [X2], AL

Отлично, большую часть мы уже сделали - реализовали алгоритм. Но вспомните постановку задачи. Там говорилось, что функция должна обрабатывать много байт, а у нас пока на входе только один байт.

Значит, можно "закрутить" код в цикл.

Для этого добавляем переменную-счётчик (предварительно загрузив значением).

Изначально счётчиком принят регистр ECX. Хотя в нашем случае это чистая условность.

dec   ECX               ; уменьшаем счётчик
js    Hex_Fin           ; если уже меньше нуля, то прыг

Такая пара команд в начале цикла обеспечивает выход из него.

Команда DEC изменяет флаги, и если до вычитания единицы в регистре ECX был 0, то после этого действия значение ECX будет FFFFFFFFh (-1). Тогда DEC поднимает флаг знака (SF=1).

Команда JS выполняет переход, только если флаг SF=1.

Почему выход лучше делать именно в начале цикла, а не в конце? Каких-то сверхважных причин нет, но так мы убиваем ещё двух маленьких зайчат (для защитников природы: в переносном смысле!).

1. Проверяем: а вдруг в счётчике уже на входе был ноль и тогда ничего не нужно считать. Это даёт стабильность функции и скромную оптимизацию по скорости всей программы.

2. Условный переход в этом месте выполнится только один раз за время работы цикла. Дело в том, что условные переходы дают бОльшие задержки, чем безусловные (это связано с возможностью предварительной загрузки следующих команд). Разумеется, всё зависит от конкретного ЦП, так что рекомендация слишком обобщённая... Но она существует. =)

Вот конкретный пример возможной ошибки на один.

ECX - счётчик, но счётчик чего?

Есть два варианта: счётчик адресов или счётчик количества.

Ошибка может возникнуть, если "кто-то" вдруг решит, что в счётчик надо загружать относительный адрес последнего байта.

Тогда "кто-то" будет высчитывать значение счётчика так:

адрес последнего байта строки минус адрес нулевого байта строки.

В итоге товарищ "кто-то" потеряет один байт.

Лучше сразу чётко задокументировать: этот счётчик - количество байт (от единицы).

Теперь можно зациклить алгоритм, добавив в конце команду "JMP на начало". Но тогда в цикле будет постоянно обрабатываться всё то же a, и сохраняться он будет в X₁, X₂ до тех пор, пока счётчик не станет меньше нуля.

Чтобы исправить это, нужно постоянно увеличивать указатели на a и X.

И вот как мы поступим.

Перед входом в цикл загрузим адрес a в регистр источника - ESI.

X₁, X₂ тоже представим одним указателем в регистре приёмника - EDI.

mov   ESI, offset a
mov   EDI, offset X

И в ходе вычислений будем увеличивать эти указатели после каждого прохода цикла.

inc   ESI
add   EDI,2

EDI изменяется на два за проход, потому что он представляет сначала X₁, а затем X₂.

Можно считать, что функция готова. Соберём всё воедино и оформим по правилам API-функций.

Для проверки работоспособности вставим всё это в готовый пример prax12.asm:

      .586
      .model flat, stdcall
      option casemap :none   ; case sensitive
;#########################################################################
      include \masm32\include\windows.inc
      include \masm32\include\user32.inc
      include \masm32\include\kernel32.inc
      includelib \masm32\lib\user32.lib
      includelib \masm32\lib\kernel32.lib
;#########################################################################
    .data
    HexBytes db 0E5h,0DCh,0BAh,98h,76h,54h,32h,10h,0Fh,0Eh,0Dh,0Ch,0Bh,0Ah,09h,08h
    
; Константа NBytes на предварительном этапе компиляции будет равна длине переменной HexBytes:
    NBytes = sizeof HexBytes             
; Будущая текстовая строка длиной HexBytes*2 
; (так как на выходе будет в 2 раза больше), +1 байт 00 на конце строки.
; Заполняем BBh только для наглядности в отладчике:
     sResult byte NBytes*2+1 dup (0BBh)  
  MsgCaption db "Результат перевода",0   ; Заголовок сообщения

;#########################################################################
    .code
start:
; вызов нашей функции представления hex-значений в тексте
push NBytes            ;количество байт для обработки
push OFFSET HexBytes   ;адрес hex-значений
push OFFSET sResult    ;адрес строки для заполнения
call ASCIIzHEX
invoke MessageBox, NULL, addr sResult, addr MsgCaption, MB_OK 
invoke ExitProcess,0   ;вызов API-функции выхода
;-------------------------------------------------------------------------
ASCIIzHEX proc pString:DWORD,pHex:DWORD,Count:DWORD      ; начало и аргументы функции
; Вход:  
; pString - указатель на строку, которую будем заполнять 
; pHex    - указатель на hex-значения                   
; Count   - количество байт для обработки               
; Выход:  ничего
push ECX
push EDI
push ESI
mov   ECX, Count
mov   ESI, pHex
mov   EDI, pString
loopHex:
    dec   ECX                 ;уменьшаем счётчик
js  HexFin                    ;если уже меньше нуля, то прыг

    movzx EAX, byte ptr [ESI] ;допустим, AX = 00E5h
    rol   EAX, 4              ;AX = 0E50h
    ror    AL, 4              ;AX = 0E05h

    cmp    AH, 9              ;сравниваем с девятью
jbe DecDigit                  ;если не больше, то прыг
    add    AH, 7              ;иначе корректируем символы от A до F
DecDigit:
    add    AH, 30h            ;получаем код символа
    mov [EDI], AH             ;сохраняем результат

    cmp    AL, 9              ;сравниваем с девятью
jbe DecDigit2                 ;если не больше, то прыг
    add    AL, 7              ;иначе корректируем символы от A до F
DecDigit2:
    add    AL, 30h            ;получаем код символа
    mov    [EDI+1], AL        ;сохраняем результат
    add   EDI, 2              ;увеличиваем указатель строки на 2
    inc   ESI                 ;увеличиваем указатель исходного байта на 1
jmp loopHex

HexFin:
mov byte ptr [EDI],0          ;в конце строки не забудем добавить байт 00
pop ESI
pop EDI
pop ECX
ret
ASCIIzHEX endp                ;конец функции
;-------------------------------------------------------------------------
end start                     ;конец программы

Тело функции занимает 65d байт. Это легко узнать либо из листинга компилятора, либо прямо в отладчике (в OllyDbg двойной щелчок по адресу нулевой команды функции даст относительный отсчёт смещений).

Если бы мы писали под FASM, можно было бы смело без изменений алгоритма выкинуть ещё шесть байт. Да и тело функции там удобнее оптимизировать. Но так ли это важно?

На моём компе эта функция формирует строку:

0E5h,0DCh,0BAh,98h,76h,54h,32h,10h,0Fh,0Eh,0Dh,0Ch,0Bh,0Ah,09h,08h

за ~154 такта. То есть каждый байт обрабатывается ~10 тактов.

А теперь вспомните, какая тактовая частота у вашего ЦП? =)

Конечно, мы сейчас сделали далеко не самую быструю и не самую маленькую из подобных API. И всё-таки приятно сознавать, что наша реализация работает в разы быстрее, чем универсальная wsprintf (распространённое табличное решение, основанное на командах XLAT, тоже почти в два раза медленнее).

Будет очень хорошо, если вы сможете написать собственную функцию для решения такой же (или почти такой ;) задачи.

Даже если ваша версия будет хуже по всем показателям, всё равно это будет хорошая работа!

Ну а если сумеете обойти меня по скорости или по размеру прямо сейчас - респект передам лично.

=)

Как измерять количество байт, вы уже знаете. Но может возникнуть вопрос, как померить количество тактов, затраченных на вычисления? Для этого существует специальная команда RDTSC (read time stamp counter), она передаёт счётчик тактов процессора в пару регистров EDX_EAX. Но в многозадачной среде Win32 правильно её использовать не так-то просто.

7. Числа в позиционных системах с разным основанием

Любое число, записанное позиционным методом, можно развернуть в математическое выражение:

an - 1 * pn - 1 + a n - 2 * p n - 2 + . . . + a1* p1 + a0 * p0

По сути перед нами общая формула получения количества из числа, представленного в некоторой системе счисления.

Здесь:

р - основание системы счисления,

а - количество в текущей цифре данной системы счисления,

показатель степени - разряд данной цифры.

Посмотрите конкретный пример.

512 в десятичной системе можно представить так:

500 + 10 + 2

А можно и так:

5*102 + 1*101 + 2*100

Лично мне было сложно переварить эту формулу.

8. Бит

Новое значение древнего слова bit, которое часто употребляется как мелкий, или частичка, уже должно было стать вам почти родным (по крайней мере, в связи с моим ником ;).

Как вы уже знаете, состояний "ДА" и "НЕТ" хватает для ответа на очень многие вопросы. Собственно говоря, такие вопросы называются односложными.

На этой базе в XIX веке Джордж Буль (George Boole) построил свою логику, из которой впоследствии вытекло целое направление алгебры - Булева алгебра. Именно она является математической базой битовых вычислений.

Например, недавно мы разбирали вопрос:

А это значение может быть отрицательным?

И как выяснилось, в каждом числе ответ даёт всего лишь один знаковый бит.

- Бинарники поручают нести флаг только самым достойным. Их имена входят в историю навечно. Любой, кто покушается на эту традицию, - личный враг каждого бината!

- Иерархия двоичного общества совершенно непривычна людям. Достойным может быть и стар и млад. И не дай Бог вам снисходительно потрепать по головке малыша бината с флагом.

Да-да, оказывается, младший бит тоже заслуживает собственного имени.

Ещё в первом классе нам объяснили (кто ж такое упомнит), что чётное число - это то, которое делится на два без остатка и каждое второе натуральное число - чётное.

Ага, раз биты - двоичные числа (один разряд - два значения), значит:

Число всегда чётное, если в нём младший бит=0.

Число всегда нечётное, если в нем младший бит=1.

Только не стоит называть его "битом чётности", потому что так принято именовать специальный бит, выделенный для контроля чётного или нечётного количества единичек в блоке. Но эта история для другой главы.

Мне кажется, можно было бы обозначить бит номер 0 как "бит нечётности", ведь состояние 1 означает нечет. С другой стороны, в этом нет особой необходимости.

И всё-таки, почему же именно двоичные числа в основе нынешнего цифрового мира?

Нет никаких причин, кроме технических условий.

Благодаря реле, электронным лампам и транзисторам, появилась возможность пропускать электрический ток в цепях с большим количеством двоичных переключателей.

Поэтому и сегодня выпускают всё новые и новые цифровые машины, основанные на двоичной системе.

Фактически инженеры готовы построить машину на любой базе, лишь бы под рукой были массовая технология и математическое обоснование.

- Бинарники очень гордятся своей победой над трилянами, но не любят обсуждать это среди чужих.

- Их Великий Бион, пророк и сын Отца небесного, предсказал конец двоичной цивилизации и призвал покончить с захватнической войной против трилян, за что и был размагничен много лет назад.

Собственно говоря, само слово впервые прозвучало не так давно.

В июле 1956 года Вернер Бухольц (Werner Buchholz) публично применил собственное словечко "byte" в докладе "О преимуществе слов длиной 64 бита для IBM Stretch".

Незадолго до этого (в 1952 г.) было организовано ""американское агентство секретов"" (The National Security Agency, NSA). Главная задача этой организации - контроль над развитием информационных технологий. Поэтому неудивительно, что к её рекомендации создавать 8-битные ячейки разработчики ЭВМ прислушались сразу же. А ведь раньше машины делали с единицами памяти по 7, 6 и даже по 4 бита (и стоило всё это сотни миллиардов $ =).

Кто конкретно разработал рекомендацию восьмибитных ячеек, достоверно узнать мне не удалось (обратите внимание на название организации =). Но зато общеизвестно, что проект IBM Stretch, который вёл Фредерик Брукс (Frederick P. Brooks), доказал всем удобство байта со значениями от 0 до 255d.

Дело в том, что в системах с двоичной логикой лучше выравнивать всё до степени двойки.

Как и люди, машины "любят" круглые числа:

10b    = 2
100b   = 4
1000b  = 8
10000b = 16d

А ещё люди любят символы.

Для того чтобы в одну ячейку можно было закодировать любую букву латинского алфавита, цифру, знак препинания или математический символ, нужно минимум 50 значений.

50d = 110010b

Как видите, 6 двоичных разрядов хватает.

Но, во-первых, уж больно маленький запас (всего 13 значений свободны), а во-вторых, 6 - не степень двойки.

16-битная кодировка даёт нам 65 536 значений, что по тем временам было бы слишком расточительно.

И хотя 7-битная система символов долго сопротивлялась, свет сошелся клином на восьми.

Далее быстро распространилось шестнадцатиричное представление байт. Причина проста.

Как мы уже убедились из прошлого примера этой статьи, hex-система имеет очень интересное свойство.

Каждый разряд кодируется в 4 бита (в тетраду). Один байт - ровно два разряда. Практично.

Представим, что a указывает на ячейку памяти c адресом 7 (восьмую по бытовому счёту).

Тогда, к примеру, ячейка с абсолютным адресом 9 будет иметь адрес 2 относительно a.

Примерно так:

                                   a         a+2
0    1    2    3    4    5    6    7    8    9
*----*----*----*----*----*----*----*----*----*----...

От a до a+2 мы имеем:

a+0

a+1

a+2

Такие адреса называются относительными.

Выходит, что когда мы видим термин относительная адресация и не видим a, нужно сразу разузнать, от чего ведётся отсчёт, иначе могут быть ошибки.

Относительная адресация поддерживается большинством команд в которых есть обращение к памяти. Пример:

mov   [EBP+8], Y

Здесь непосредственное значение 8 является относительным адресом от указателя в регистре EBP. То есть a будет именно EBP.

Также для формирования указателя можно использовать два регистра:

mov   [EBP+ECX], Y

Давным-давно (примерно в 1950 году), когда компьютер был простым программируемым калькулятором, обращаться к памяти по физическому номеру ячейки было довольно удобно (и номеров было немного, и программа выполнялась одна). Но как только "калькулятор" стал мощнее, инженеры задумались, как бы поместить в оперативную память не одну программу, а сразу несколько.

Проблема вот в чём: допустим, после компиляции есть такая команда:

mov  [100h], EAX

В квадратных скобках указан адрес, по которому будет размещено значение EAX.

Если в памяти одна программа - проблем нет. Ячейка 100h может принадлежать только ей.

Но как разделить память между большим количеством приложений?

Самое тупое решение - при кодировании заранее определять, где программа физически будет располагаться в памяти. Допустим:

приложение XXX пишется под адреса от 0 до 1000h

а YYY будет всегда от 1000h до 2000h

и т.п.

Представляете, как дрались бы программисты за кусок памяти? =)

Кроме того, если мне не нужна XXX-порнография, то что: в моём компе не будет использоваться часть памяти от 0 до 1000h? =/

Не-е, так не пойдёт.

Давайте думать, как бы разделить физические адреса, чтоб не слишком сложно писать код программы и не слишком расточительно выделять память.

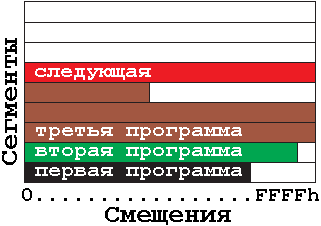
В 1960-х годах специалисты IBM распространили сегментарную модель памяти. И довольно долго рынок развивал именно эту модель. В том числе и Intel. Инженеры компании создавали ЦП 8086 и 88, а также 80286 в расчёте вот на такую организацию памяти:

Модель адресации памяти реального режима процессора

Здесь оперативка представлена в виде прямоугольника, разделённого на полоски.

Получилось довольно красиво.

У каждой программы есть своя полоска (или даже несколько). Называются такие полосы сегментами.

Внутри каждого сегмента начинается собственная адресация от нуля - смещение.

Таким образом, программист во время кодирования может вообще не заботиться, где именно физически будет размещена программа в памяти. У него есть так называемый логический адрес.

Здесь номер сегмента и смещение (полный логический адрес) определяют физическое расположение байта.

Такое устройство памяти нуждается не только в аппаратной поддержке, но и в программном управлении. Для чего и была придумана OS.

DOS управляет загрузкой и выгрузкой программ примерно так. Свободный сегмент выделяется программе во время загрузки. А после того, как программа завершилась, DOS снова помечает сегмент как незанятый.

Но давайте рассмотрим железную часть вопроса.

Мы определились, что программы используют логические адреса.

Физический адрес формируется где-то в недрах ЦПУ.

Выходит, на уровне Ассемблера обращаться к ячейкам памяти по их уникальным номерам нельзя.

Важно понять, как ЦП из логического адреса получает физический номер байта.

В прошлом витке я уже говорил, что для указания сегментов есть набор сегментных регистров процессора - CS,DS,SS,ES,FS,GS.

Все машинные команды, в которых есть обращение к памяти, обязательно работают с одним из сегментных регистров, даже если мы не указываем его в команде Ассемблера в явном виде.

Чтобы наглядно в этом убедиться, включите опцию в отладчике OllyDbg:

Alt+O > закладка "disasm" > поставьте галку на "show default segments".

Теперь вы будете видеть, к какому сегменту обращается та или иная команда.

Допустим, вот такая:

mov ecx, dword ptr ss:[ebp]

SS:[EBP] - подобная запись принята в MASM'e. В Hiew'e или FASM'е немного другой синтаксис, но главное здесь двоеточие:

сегмент : смещение

Этот принцип остаётся во всех известных мне компиляторах и дизассемблерах.

Впрочем, даже если в команде нет обращения к памяти, она ведь сама там располагается. Значит, адрес команды тоже как-то должен определяться. В прошлом витке мы узнали, что для этого есть регистр текущей инструкции - EIP. Сегодня я скажу вам - Земля не плоская!

Определить линейный адрес следующей машинной команды в памяти можно только при помощи пары регистров CS:IP в реальном режиме или CS:EIP в 32-битных режимах.

И тут опять нужно объяснить, что за линейный адрес.

В реальном режиме линейный адрес формируется очень просто:

значение сегментного регистра умножается на четыре и складывается со смещением.

CS*4+EIP = линейный адрес инструкции = физический адрес инструкции

Как видите, изначально термин линейный адрес всего лишь заменял физический адрес.

Но, к сожалению, уже в 386-м ввели многоуровневую адресацию (об этом чуть ниже).

Тут линейный адрес отошел от понятия физический. При этом фактически он перестал быть линейным (то есть одномерным).

Нынче "линейным адресом" называют двух- или даже трёхуровневое значение.

По задумке должно быть так:

Сегмент - динамическая составляющая, его выделяет операционная система.

Смещения статически задаёт программист (+компилятор) на стадии разработки программы.

Но дело в том, что легко можно написать такую программу, в которой и смещения будут изменяться динамически, и интересующие нас сегменты мы определим сами, обходя DOS. Так и делают различные зловреды. А ещё такое может произойти из-за ошибки программистов. Тогда чаще всего зависает вся система.

Простой пример записи в некий сегмент:

00000000: B82010       mov  ax,01020
00000003: 8EC0         mov  es,ax
00000005: BE5001       mov  si,00150
00000008: 26C704FFFF   mov  w,es:[si],0FFFF
0000000D: CD20         int  020

Можно сделать com-файл в Hiew'е, но последствия выполнения такого кода не известны. Хотя в системах с ядром NT вряд ли произойдёт что-то страшное.

Частичный разбор:

00000003: 8EC0         mov  es,ax

Здесь копируется значение из AX в сегментный регистр ES.

У команды MOV не предусмотрена возможность загружать сегментные регистры прямым значением (только копированием из других регистров). Можно было использовать специальную команду LES, но мне совсем не хочется загромождать статьи лишними сведениями. В ближайшее время нам всё равно не понадобится эта команда, и в кодах приложений под Win32 вы не встретите её полезного применения (только в мусорных кодах протекторов для отвода глаз).

00000008: 26C704FFFF   mov  w,es:[si],0FFFF

А вот здесь одно слово FFFFh помещается по адресу, указанному в паре регистров ES:SI.

Результатом действия такого "примерчика" будет запись значения по неизвестно кому принадлежащему адресу.

И ничто не помешает выполниться этому коду в Real Mode или в его виртуальной реализации (WinXP, DOSbox и т.п.).

Его описание довольно сложная штука.

Рынок диктует условия развития техники. Каждая следующая доработка должна поддерживать предыдущую.

Сейчас мы имеем ЦПУ, которые по большей части совместимы с прародителями 25-летней давности. Это позволяет занимать лидерство в масштабах планеты. Но обратной стороной медали является нагромождённость тех частей, которые активно развивались.

Адресация памяти пострадала больше всего. Тут такие "рога" наросли - по самый потолок!

Начнём с простого.

В PM значительно увеличился максимальный размер сегмента.

В реальном режиме смещение внутри сегмента кодируется двумя байтами, что даёт значения от 0 до 65 535 (64 килобайта), а в PM мы получили 32-битное значение для смещений, и это позволяет адресовать сегменты до 4 Гигабайт.

Следующее важное отличие - формирование физического адреса.

Для этого введены таблицы дескрипторов, а позже ещё и страничная адресация.

Эти новшества очень сильно усложнили формулу получения физического адреса. Но зато появилась возможность создавать сложные многозадачные операционные системы с простой средой для программ, что значительно упростило работу программистов.

Итак, таблица дескрипторов - это сложный вид данных.

Каждый дескриптор - 64-битная структура, описывающая сегмент,

а таблица - массив этих структур, расположенный в памяти.

Для чего нужны дескрипторы?

Вместо того чтобы явно получать адресную составляющую сегмента из регистра, в PM процессор обращается к дескриптору.

Группу регистров CS,DS,SS,ES,FS,GS впору переименовывать из сегментных в селекторные, так как теперь они хранят в себе не номера сегментов, а так называемые селекторы.

Значение каждого селектора сообщает ЦП, где конкретно взять дескриптор.

То есть в какой таблице и под каким номером его искать.

И вот уже сам дескриптор несёт в себе полную информацию о сегменте: место положения, уровень доступа, размер, принадлежность и т.д.

Устройство дескрипторов и селекторов в рамках Чтивы 0 мы разобрать не сможем, так как это слишком сложная тема. Даже то, что вы о них сейчас узнали, уже много.

Одной из последних серьёзнейших доработок защищённого режима стала страничная адресация.

Все современные ОСи используют данную надстройку над сегментарной моделью памяти.

Страничная адресация создаёт ещё один уровень трансформации от логического к физическому адресу. Давайте рассмотрим в общих чертах путь получения физического адреса в PM.

Даже если не вдаваться в конкретику битовых значений, это выглядит довольно хитро.

Получив команду типа:

mov dword ptr ds:[403000],0EEEEEEEEh

для размещения значения EEEEEEEEh, процессор сначала сформирует так называемый линейный адрес:

1. Получив из сегментного регистра значение селектора, он узнает, где брать дескриптор.
2. Из дескриптора ЦП узнает, можно ли вообще разрешать запись этого числа туда, куда просят (это ведь защищённый режим). Если можно, то из дескриптора извлекается адрес базы сегмента.
3. Дальше просто складывается адрес базы со смещением.

Всё, линейный адрес готов.

Если бы не было страничной адресации (бит PG=0), то получившийся линейный адрес был бы равен физическому. А когда бит PG=1, происходит ещё одно преобразование, вид которого зависит от различного размера страниц - 4Kb, 2Mb, 4Mb (на это влияет состояние системных битов PAE, PSE, PS, PSE-36).

Как видите, система очень запутанная. Не пытайтесь "проглотить" всё за день.

Если чувствуете, что уже готовы - вдумчиво читайте книги про архитектуру процессоров Intel (конкретных авторов советовать не буду, сам читал только одного и книгой недоволен).

А сейчас хорошо бы уточнить один важный момент.

Повторю ещё раз: Земля не круглая! Пока мы её окончательно не заутюжили.

Пускай пудрят мозги англоязычные люди со своей Flat model, а мы будем называть её сплошная модель и никак не плоская!

Самое главное, система страничной адресации даёт возможность строить большие виртуальные пространства в старом добром 32-битном режиме (4 Терабайта - это немало).

Эта возможность используется начиная с древнючей "Windows 3.11 для рабочих групп".

Вы скажете: но у меня ведь нет столько оперативной памяти, зачем мне это надо?

Для того чтобы просто осуществлять менеджмент процессов, многозадачной операционной системе нужно огромное количество виртуальных адресов. Каждый процесс имеет в своём распоряжении 32-битную адресацию, то есть 4Gb виртуального пространства. Но это только один процесс, а посмотрите, сколько их у вас сейчас запущено (Ctrl+Alt+Del > Процессы)?

И всё-таки, как быть, если в машине не хватает оперативки даже на один процесс, а тут Терабайты?

И эту проблему решает страничная адресация.

В оперативной памяти могут располагаться только те страницы, которые нужны в данный момент.

Все остальные тем временем будут лежать на диске в страничном файле (swap-file, paging-file) до тех пор, пока система не вызовет их в оперативку.

Обратите внимание в закладке "Процессы" на колонку "Память".

Из неё видно, сколько Килобайт занимают существующие страницы памяти (в оперативке + страничном файле).

Так что виртуальное адресное пространство - это всего лишь потенциальный диапазон адресации, а не реальная память.

Но давайте вернёмся к сегментам. Как Win-программы используют сегменты?

Минимально.

Сегмент само собой по-прежнему указывается в командах и по-прежнему участвует в формировании физического адреса, так как это заложено в архитектуру IA-32. Но основная работа с сегментами происходит так хитро, что как будто бы их вовсе нет.

Давайте загрузим в OllyDbg любую программу.

Обратите внимание на содержимое сегментных регистров.

Регистр DS определяет текущий сегмент данных.

SS - текущий сегмент стека.

ES - расширенный сегмент данных

Их значения почему-то одинаковые.

А это значит, что они указывают на один и тот же дескриптор.

Один дескриптор - один сегмент.

К сожалению, получить подробную информацию о дескрипторе OllyDbg не позволяет.

Если у вас есть возможность запустить SoftIce, можно посмотреть информацию из глобальной таблицы дескрипторов при помощи команды GDT.

Вот главные свойства сегмента, на который указывают ES,DS,SS:

Линейный адрес начала сегмента  = 0
Размер сегмента                 = 4Gb
Тип сегмента                    = Для данных
Уровень привилегий              = 3 
Разрядность адресов и операндов = 32 бита
Чтение/запись                   = Разрешено

Про уровни привилегий (rings) я уже говорил: для приложений =3 (user mode), для драйверов и ядра =0 (kernel mode).

Всё остальное вам должно быть более-менее ясно.

Теперь заглянем в сведения о сегменте кода, на который указывает CS:

Линейный адрес начала сегмента  = 0
Размер сегмента                 = 4Gb
Тип сегмента                    = Для кода
Уровень привилегий              = 3 
Разрядность адресов и операндов = 32 бита
Чтение/запись                   = Только чтение

Удивительное дело. Выходит, что линейные адреса двух наших сегментов перекрывают друг друга полностью.

Отличаются только тип сегмента и возможность записи/чтения.

Проведём небольшой эксперимент. Подправим одну команду в любом из Win32-примеров.

Допустим, в prax11:

	div    byte ptr [divisor] 

Заменим на:

	div    byte ptr CS:[divisor]

Пример будет работать, как будто бы ничего не изменилось.

По умолчанию операнд команды div адресуется через DS, но и в случае SS, ES и даже CS в форточках мы получим один и тот же результат.

Ура! Нам больше не нужно думать о сегментах. Если бы вы программировали серьёзные вещи в MS-DOS, вы бы поняли, какое это облегчение - так говорят наши отцы, и я им верю. =)

Но дальше ещё интереснее. Загрузите другой экземпляр OllyDbg с любой другой программой, и вы увидите ту же картину.

В регистрах ES, DS и SS будет тот же селектор. И значение CS идентично прежнему экземпляру отладчика.

Как же так получается: разные программы в одном и том же сегменте в одно и то же время... Как это работает?

Опять-таки виновата страничная адресация.

Каждая задача обладает своим набором страниц, а сегменты - "побоку" (не считая служебных мелочей).

Кстати говоря, у каждой страницы тоже есть свойства (чтение/запись, разрядность адресов и операндов...).

=)

Самое сложное в этом деле то, что страничная адресация управляется больше программно, чем аппаратно.

То есть именно Форточки разруливают своё виртуальное пространство, а ЦП лишь предоставляет некоторые средства.

Вот и получается: вместо того чтобы разделять задачи по сегментам, ОСь создаёт наборы страниц.

Тут без глубоких исследований недр ОСи не обойтись. А как известно, устройство ядра WinNT - секретная информация. =) Один небезызвестный богатый дяденька может и в суд подать за разглашение его великого ноу-хау. =)

Отложим вопрос о многозадачности на далёкое потом.

Больше не будем говорить о физических, линейных и логических адресах. Рекомендую про них пока вообще не думать. Пусть уляжется нулевая волна непонимания (помните, как было трудно знакомиться с регистрами общего назначения, и ничего - улеглось ведь).

Дальше в Чтиве 0 мы, как и раньше, будем употреблять слово адрес в значении смещение (его ещё называют эффективный адрес). Это ни капельки не помешает нам писать любые программы.

Что же мы имеем в этих на вид бесконечно просторных 4Gb?

Сразу скажу, старшая половина (без ключа /3Gb) принадлежит только операционной системе.

Так что остаётся 2Gb в диапазоне от 0 до 7FFFFFFFh.

Вы уже могли убедиться, что код и данные исполняемого модуля располагаются довольно далеко.

Откройте какой-нибудь пример в OllyDbg и взгляните на карту памяти процесса (Alt+M).

1. В левой колонке - адрес нулевого байта данного блока памяти.

2. Далее - размер блока.
Напомню вам про ошибку на один. Если сложить адрес нулевого байта и размер, мы получим адрес байта, следующего за этим блоком, а не последнего в блоке! Как я уже говорил, не путайте размеры с адресами.

3. Если блок принадлежит образу запускаемого модуля (exe или dll), то следующая колонка сообщает имя этого файла.

4. Опять же, если речь идёт об образе dll или exe, мы можем узнать имя секции, размещённой в данном блоке, из колонки - сами догадайтесь, с каким именем.

5. Затем Olly выдаёт нам краткую информацию о содержимом блока.

6. Тип блока может иметь такие значения:
Priv - Блок занят данными неопределенного типа.
Map - Блок занят прямой или косвенной проекцией файла (Memory Mapped File).
Imag - Блок занят образом PE-модуля
Свободные адреса просто не отображаются

7. Колонка "Access" должна показывать текущее состояние доступа для страниц памяти данного блока.
Должна, только не всегда это делает. В OllyDbg 1.10 эта колонка неправильно отображается. В версии 2.0 ошибки нет.
В колонке возможны следующие варианты:
пустота - блок недоступен
R - доступен только для чтения
RW - разрешено чтение/запись
R E - разрешены запуск кода и чтение
RWE - полный доступ (чтение, запись, запуск)
Guarded - блок, для которого генерируется специальное исключение при записи (это не значит, что запись запрещена)
CopyOnWr - в случае записи страница, которую изменили, будет отделена от файла
Всё это атрибуты защищённого режима (фактически битовые флаги из дескрипторов и таблиц).
Последний атрибут вообще очень хитрый. Включение такого метода позволяет экономить ресурсы системы.
Те страницы памяти, которые не меняются, так и остаются связанными с файлом. Но как только мы выполним команду типа "mov [offset],1", страница, на которую указывает offset, будет полностью скопирована. Так что оригинальный файл образа остаётся нетронутым.
Пункт контекстного меню "set access" позволяет менять основные условия доступа, но поскольку колонка отображается некорректно, вы не увидите результат изменения атрибутов (или увидите неправильно). Однако само изменение происходит. А если по каким-то причинам отладчик не может изменить доступ, в строке состояния промелькнёт предупреждение об этом.

8. Колонка "Initial Access" должна показывать начальное состояние доступа для страниц памяти данного блока.
Опять это слово "должна" и опять оно актуально для версии 1.10. В 2.0 ошибки нет.
В этой колонке отображаются атрибуты чтения, записи, запуска (R,W,E соответственно).
Если блок принадлежит образу PE-файла, то эта колонка должна заполняться из атрибутов секций файла.
Но отображается колонка некорректно.

9. В последней колонке "Mapped as" содержится путь к проецируемому файлу.
Файловая проекция - это механизм обращения к файлам. В ближайшее время мы рассмотрим, как его использовать на практике.

Постарайтесь не пугаться такого большого количества атрибутов и разных типов.

Физически почти вся эта информация кодируется всего лишь в битовых флагах (один бит - одно значение). И хотя все биты разбросаны по таблицам, регистрам и каталогам защищённого режима, со временем мы познакомимся с ними и даже научимся переключать (так чтобы система не упала... или хотя бы не всегда падала =).

Несмотря на то, что в разных версиях Форточек адресное пространство процесса может выглядеть по-разному, довольно полезно знать, где что может располагаться в памяти вашей системы.

Рекомендую хотя бы в общих чертах ознакомиться с диапазонами адресов. Загружая в отладчик разные программы, вы можете убедиться, что основная картина остаётся неизменной.

Ещё хочу добавить:

• адреса от 0 до 0000FFFFh зарезервированы для отлова ошибочных указателей (это помогает избежать частых ошибок адресации в никуда);
• все образы exe- и dll-файлов располагаются от 00400000h и до 7FFEFFFFh;
• и старшие 64Kb пользовательского режима (user mode) от 7FFF0000h до 7FFFFFFFh закрыты для большей стабильности ядра.

Ночь была очень тяжелая, некоторые так нервничали из-за предстоящего испытания, что не могли заснуть. Немного побродив, они собрались в кучку, в результате не выспались все.

Однако чем выше поднималось светило, тем больше радостных криков доносилось с берега.

Компания явно разыгралась. К полудню пляжные уже забыли про вечернее испытание. Кто-то на спор нырял за зелёными ракушками, кто-то прыгал в длину с ног на руки и потом на другие ноги, а один парень, забравшись на высокую пальму, пытался разглядеть соседние острова, но вокруг была только вода.

Когда прозвучал сигнал, большинство новобранцев уже давно были в главном зале, нервно ожидая этой минуты.

Здесь было как-то необычно тихо без семёрки раздолбаев.

Вошел куратор и с невозмутимым видом предложил всем выйти к берегу, где как раз в этот момент опоздавшие спешно переодевались.

1. А какой сейчас идёт год? Я имею в виду от Рождества Христова.

2. Соответственно, когда закончилось второе тысячелетие?

3. Вообразим, что мы проектируем устройство двоичного компьютера.

И вот речь зашла о представлении отрицательных чисел, кто-то предложил сделать дополнительное кодирование с двумя нулями - положительным и отрицательным.

Тогда каждый байт будет представлять:

Hex-значения:            FF,FE,FD.............  80|7F ............1,0
Dec-значения со знаком:  -0,-1,-2.............-127|127............1,0

Автор был доволен таким решением, потому что на первый взгляд симметрия не нарушается нигде. Смена знака будет выполняться простым отражением битов (без всяких +1).

Объясните, почему эта идея не очень хорошая.

4. ...Хорошо, но ведь в той же математике определено, что младшее целое положительное число - единица. Пусть тогда в этой машине ноль представляется хотя бы только отрицательным:

Hex-значения:            00,FF,FE,FD..........  81|80 ............1
Dec-значения со знаком:  -0,-1,-2,-3..........-127|128............1

Объясните, в чём преимущество системы с нулём, условно приписанным к положительному ряду чисел.

5. Сколько байт будет занимать число 12345d в непакетированном десятичном представлении? А в пакетированном?

6. Нужно представить числовые значения в текстовой строке для Win32. Сколько байт будет занимать строка в следующих случаях:

• hex-число размером dword;
• пакетированное dec-число, занимающее в памяти 7 байт;
• непакетированное dec число 9 байт;
• знаковое десятичное, занимающее в памяти dword.

7. Сколько раз вы прочитали эту статью?

- Ну что ж, Юнга, отвечал ты сумбурно, кое-что напутал, но по счастливой физиономии вижу - обучение идёт не впустую. У меня больше вопросов к тебе нет...

Задача 1. Один алгоритм из этой статьи не был представлен примером на Ассемблере. Попробуйте на его основе самостоятельно написать функцию.

Постановка задачи

Написать такую функцию, которая будет принимать DWORD и возвращать указатель на текстовую ASCIIz строку с десятичной записью натурального числа.

То есть функция должна переводить 32-битное значение по следующей схеме:

00000000h > 30h,30h,30h,30h,30h,30h,30h,30h,00 (или просто 30h,00)
00000001h > 30h,30h,30h,30h,30h,30h,30h,31h,00 (или просто 31h,00)
...
00000010h > 30h,30h,30h,30h,30h,30h,31h,36h,00 (или просто 31h,36h,00)
...
FFFFFFFFh > 34h,32h,39h,34h,39h,36h,37h,32h,39h,35h,00

Оформить можно так:

Вход:  EAX = число для перевода;
       EBX = указатель на буфер для строки.

Выход: EAX = указатель на готовую строку.

Задача 2. Теперь сделайте то же самое, только запись числа должна быть в системе с основанием от 2 до 16d.

Задача 3. Предполагается, что вы сейчас реализовали цикл, основанный на целочисленном делении. Теперь давайте попробуем обратное действие - умножение (команда mul). Постарайтесь самостоятельно сделать функцию перевода ASCIIz-строки с натуральным десятичным числом до 4294967295 в DWORD-значение.

Постановка задачи

• Функция должна сделать из символов десятичных цифр в ASCIIz-строке двоичное DWORD-значение.
• В самой строке допускаются любые символы.
• А значит, строка может быть произвольной длины.

Буду ждать ответы на bitfry )собак( mail.ru

1.

Исходные: на календаре число 2007, все вычисления в десятичной системе.

Попробуем понять, сколько полных лет прошло от Рождества Христова.

Надо сказать, что задача эта вовсе не простая. Её можно расписать через относительную адресацию.

Будем рассуждать.

Когда рождается человек, мы говорим: начался его первый год жизни (но ещё не закончился).

Назовём a - день рождения человека, тогда в следующий раз люди будут отмечать годовщину в a+1 год:

    a+1                                          a+10
a    1    2    3    4    5    6    7    8    9   10
*----*----*----*----*----*----*----*----*----*----*...

Вот мы празднуем десятилетие человека (a+10 лет).

В этот день мы скажем: десять полных лет. Начался одиннадцатый год жизни.

Тогда в a+2007 лет мы скажем: парень, как тебе это удалось!? Ты уже прожил 2007 лет и начал жить 2008-й год:

    a+1          /                                       a+2007
a    1    2    3 \ 1999 2000 2001 2002 2003 2004 2005 2006 2007
*----*----*----*-/---*----*----*----*----*----*----*----*----*-...

Если предположить, что для Бога мы использовали тот же метод, что и для себя, то сейчас прошло полных 2007 лет. И начался 2008-й год.

Ведь датировка календаря должна была начаться от a, то есть от Рождества Христова (расхождения из-за астрономических поправок учитывать вообще не будем).

Но такие рассуждения можно оспорить.

Дело в том, что добрые люди, писавшие Библию, забыли упомянуть дату рождения Христа.

Наверное, по большому счёту они были правы. Ведь даты - не самое важное в жизни.

Но потом, спустя приблизительно полтысячи лет, другие добрые люди всё же решили договориться, от чего вести отсчёт календаря. Оказалось, довольно трудно определить хотя бы общепринятый год Рождества.

И вот тут вполне могла появиться ошибка на один. Дело в том, что в те времена позиционный метод счёта ещё не получил должного распространения. Большинство записей тогда вели римскими цифрами (вспомните, что даже сегодня века записывают римским способом). В римской системе счисления не было нуля. Первая цифра, с которой начинался счёт, была I. Так что Новую эру вполне могли отметить как год I. Вполне логично, так как мы точно знаем, что записали и день I, и месяц I.

Тогда датировка смещается на а=1, и число 2007 на календаре совпадает с числительным две тысячи седьмого года.

К сожалению, найти исторические документы по данному вопросу к моменту публикации статьи я так и не смог.

2.

Из попытки решить первую задачу вытекают возможные ответы:

если датировка ведётся согласно годам жизни Христа, то второе тысячелетие Новой эры закончилось в момент перехода с 31.12.1999 на 01.01.2000;

если Новую эру отметили единицей, то с 31.12.2000 на 01.01.2001.

Христиане отмечали приход третьего тысячелетия в ночь на 01.01.2000, о чём неоднократно говорилось в официальных поздравлениях глав различных конфессий.

Президиум РАН придерживался той же точки зрения.

Однако многие юридические документы (где годы прописаны буквами) могли бы стать недействительными, если бы эту точку зрения подтвердила организация, ответственная за датировку в нашем государстве (и не только в нашем).

И вот что получается официально: Межведомственная комиссия по времени и эталонным частотам при Госстандарте России заявила, что в России с 1918 года действует григорианский календарь, согласно которому новый век и третье тысячелетие начались 1 января 2001 года. При начале летосчисления Новой эры нулевого года не существовало, поэтому все десятилетия и столетия начинаются с 1 января года, следующего за окончанием десятого и сотого годов.

Предлагаю вам пару ссылок по теме:

Задача 1.

Функция представления DWORD-значения натуральным десятичным числом в ASCIIz-строке.